Hello Readers,
 Today we will discuss time series in this post. We will be using the AirPassengers data set available in R. It describes the monthly ridership of international airline passengers from 1949 to 1960.
Today we will discuss time series in this post. We will be using the AirPassengers data set available in R. It describes the monthly ridership of international airline passengers from 1949 to 1960. We will perform time series decomposition of the data to gain a better understanding of the airline passenger patterns (trend, seasonal, cyclical, long-term, residual, etc.) during that time. This is the first part of the 'Time Series' series (we will conduct series forecasting later).
Open R, and let us get started!
The Time Series Class
To begin, R has a class of objects especially for time series analysis. They are designated as ts (click me!), which are data sampled at equidistant points in time. Below is an example of a time series. It has values from 1 to 30, repeating 12 times indicating by month, starting from year 2011 in the third month, March. The attributes() tells us the properties of the time series and the class.
 |
| Sample Time Series |
Call attributes() and str() on AirPassengers to see what we are working with. The attributes show the low and high time values (1949.000, 1960.917) followed by the interval between the data values (12.000). Usually an interval of 7 represents weeks, 12 means months, and 4 means yearly quarters, so here, the AirPassenger data is measured monthly.
 |
| Attributes and Structure of AirPassengers |
Next, the structure informs us of the value numbers (1 to 144), the years (1949 to 1961), and then the actual passenger volumes, in thousands starting from 112, 118, 132, and so on. We can also visualize the data with a simple plot:
 |
| Basic AirPassengers Plot |
Now that we have a good grasp of the ts() object and the data set we will analyze, it is time for the decomposition process.
Time Series Decomposition
Fantastic. But what is decomposition? Simply put, decomposition breaks down a time series into components- such as trend, seasonal, cyclical, and irregular (see Note at end). Trend refers to the long term trend, seasonal is seasonal variation- fall, winter, etc. Cyclical means repeated fluctuations, that are non-periodic, and the irregular component refers to abnormal fluctuations, also known as residuals.
- Time Series Data = Seasonal Effect + Trend + Cyclical + Residual
First, create another time series set with ts(), apts (short for AirPassengers Time Series) with a frequency of 12. This set will start at a default year 1 with the AirPassengers numbers. The decompose() function will yield a list containing the various components below. Take note of the class name.
 |
| apts Time Series Decomposition |
The apts.de is a decomposed.ts class object, with various vector measurements of the components. For example, we can look at the estimated seasonal decomponent in apts.de$figure, and see that in the 11th month, November, there was a low seasonal factor of -53.59, and in July (7) there was a high seasonal factor of 63.83. It appears that airline ridership peaks in the summer and fall months and falls during the winter.
 |
| Plotting Seasonal Decomponent |
Naturally, we can visualize the seasonal factors with the above code to yield a graphic. And yes, it looks as if the airlines are really popular in the summer- makes sense for vacation time (in North America)!
 |
| Seasonal Factors |
We can also plot the all the components together with the observed time series in a single plot. Notice that the over all trend is increasing, the seasonal factor peaks during summers, and there is more fluctuation in the earlier and later years in the data than the middle. It is obtained after removing the long term trend, and seasonal factors from the data.
 |
| Decomponents Plot |
Seasonal Factors Adjustment
Also, we can adjust the AirPassengers data now that we have some decomposition factors. Let us adjust for seasonality. Begin with the original AirPassengers data to have the years intact. Next, use the decompose() function to obtain the components. Next, subtract the seasonal factor from the original data into another data set and label it appropriately.
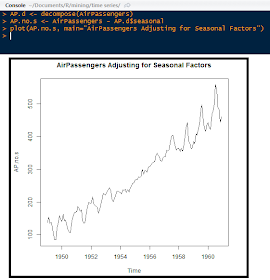 |
| Seasonal Factors Adjustment Code and Plot |
After plotting the adjusted data, we can observe how from the end of 1953 to middle of 1956 there is little fluctuation compared to the earlier and later years. Because we adjusted for seasonality, that means from '53 to '56 much of the fluctuation was due to differences in season, whereas the years prior to 1953 and after 1956, the fluctuations are not really influenced as much from season time.
This is shown by how after the seasonal factors were removed from the time series, the ridership from 1953 to 1956 increased more stably. It appears that passengers were not influenced as much by the season in which to fly before 1953 and after 1956.
Note:
This decomposition assumes that the time series is calculated as an additive model as opposed to an multiplicative model, where the components are multiplied together. Multiplicative models are considered when the absolute differences are less important than the proportional differences in a time series. For example, if we had a time series of exponential growth of bacteria, or price inflation, the proportional change can be overlooked when the absolute values are smaller using an additive model. The decompose() function can be modified with a type="multiplicative" argument for a multiplicative model. The multiplicative model is shown below. We can just take the logarithms of each side and then the components act as an additive model.- Time Series Data = Seasonal Effect * Trend * Cyclical * Residual
- Into:
- log( Data) = log(Seasonal Effect) + log(Trend) + log(Cyclical) + log(Residual)
And there we have it! This concludes time series decomposition for now. There are more advanced functions for time series, such as stl() which we will cover in later posts. But for now, the next post in the series will move on to time series forecasting.
Thanks for reading,
Wayne
@beyondvalence
The seasonal pattern gets stronger with increasing time. Your conclusion "that from '53 to '56 much of the fluctuation was due to differences in season, whereas the years prior to 1953 and after 1956, the fluctuations are not really influenced as much from season time" is misleading.
ReplyDelete