Hello Readers,
This post will delve into RSA encryption, discovered by Ron Rivest, Adi Shamir, and Leonard Adleman in 1977. However four years prior, in 1973, English mathematician Clifford Cocks already discovered the method but it remained classified until 1997.
| Public and Private Keys |
The RSA cryptosystem was one of the first public-key systems widely used for secure data transmission. Let us use a bank as an example. For secure transfers, the bank makes a public key available to bank users to encrypt their banking data, instead of giving each user a separate independent key. This streamlines the amount of data the bank handles, and occurs in the background when users accesses their online accounts. The bank holds the secret private key, which can decrypt the encrypted data to verify the user identity. Even if a malicious third party obtains the encrypted data and has the public key, the lack of the private key renders the decryption unfeasible through brute force.
RSA is considered an one way function, where the encryption is simple but the reverse, decryption is fairly difficult and/or time consuming. (Here's one ingenious way to crack the algorithm.)
Let us see how to accomplish this one way function in R.
Generating Public and Private Keys
First, we need to figure out how the one way function works. We require two items: prime factorization and a function that depends on it. Euclid discovered that any integer has one set of prime factors. This is important because finding prime factors takes exponentially more time than multiplying equally large numbers.
Euler discovered the phi function where the phi of integer N gives the number of integers less than N which does not share any factors with N (so phi(8) = 4). Finding the phi of prime numbers is relatively easy as the prime N is the only similar factor, so the phi of a prime number is simply prime-1. It follows that the phi of the product of 2 prime numbers is simply phi(p1*p2) = (p1-1)*(p2-1).
Connecting this together is Euler's theorem with a and n co-prime integers, a ^ phi(n) is congruent to 1 (mod n). We can use two prime numbers in our phi function to create a difficult code to break unless the user knows the prime numbers, due to the difficulty of prime factorization. Since we pick the prime factors first and multiply them to obtain the public key, it is relatively easy for us.
To continue the process we need to create an exponent involving phi. We pick an arbitrary public key e, whose value is less than n, and is coprime with our pre-specified prime factors. This will be our encryption exponent. Our private key, d or decryption exponent, will be (2*phi(n)+1)/e. This is the result of manipulating Euler's theorem so that a ^ 2*phi(n)+1 is congruent to a (mod n).
a ^ e is congruent to c (mod n), and converting c back to a, we use c ^ (2*phi(n)+1)/e which yields a (mod n).
Some sample values are shown below:
 |
| Sample Values |
Calculating the Modulus
Right off the bat if we try to find the remainder of 5^55 mod 221, we see that R gives us a warning message because the numbers are so large. Just look at 5^55! 38 zeros! There has to be another way of calculating the modulus.
 |
| Warning! |
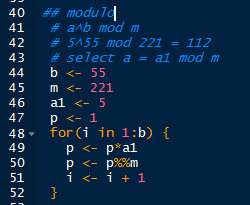 |
| Modular Algorithm |
 |
| Success! 112 |
The Encrypt Function
For these following functions, we will use the sample values as shown again below.
 |
| Sample Values |
 |
| Encryption Function |
 |
| Encrypted Message, 154827 |
The Decrypt Function
Keeping in mind the sample values, they are posted here again.
 |
| Sample Values |
 |
| Decrypt Function |
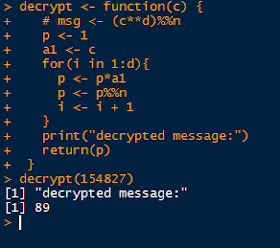 |
| Decrypted Message, 89 |
Note that we used the private key to decrypt the message. Someone with the public key would be hard pressed to factorize the large n into prime factors: in 1999, a 512 bit, 155 decimal digits, factorization was performed in 6 months- quite a long time! The current record is 768 bit integer factorization in 2009, taking 4 years.
Gmail and Facebook use 1024 bit encryption and Twitter uses 2048 bit (many upon many digits). Here is a video on YouTube about RSA.
Hope you guys liked this scenic detour from data analysis and into cryptography. Stay tuned for more R!
Thanks for reading,
Wayne
@beyondvalence
No comments:
Post a Comment