Hello Readers,
 The last time we used random forests was to predict iris species from their various characteristics. Here we will revisit random forests and train the data with the famous MNIST handwritten digits data set provided by Yann LeCun. The data can also be found on Kaggle.
The last time we used random forests was to predict iris species from their various characteristics. Here we will revisit random forests and train the data with the famous MNIST handwritten digits data set provided by Yann LeCun. The data can also be found on Kaggle.We will require the training and test data sets along with the randomForest package in R. Let us get started. (Click here for the post that classifies MNIST data with a neural network.)
Scribbles on Paper
Hand writing is unique to each person, and specifically the numbers we write have unique characteristics (mine are difficult to read). Yet when we read numbers written by other people, we can very quickly decipher which symbols are what digits.
Since there is increasing demand to automate reading handwritten text, such as ATMs and checks, computers must be able to recognize digits. So how can we accurately and consistently predict numbers from hand written digits? The data set provided by Yann LeCun was originally a subset of the data set from NIST (National Institute of Standards and Technology) sought to tackle this problem. Using various classifier methods LeCun was able to achieve test error rates of below 5% in 10,000 test images.
The data set itself consists of training and test data describing grey-scale images sized 28 by 28 pixels. The columns are the pixel number, ranging from pixel 0 to pixel 783 (786 total pixels), which have elements taking values from 0 to 255. The training set has an additional labels column denoting the actual number the image represents, so this what we desire from the output vector from the test set.
As we can see, the image numbers are in no particular order. The first row is for the number 1, the second for 0, and third for 1 again, and fourth for 4, etc.
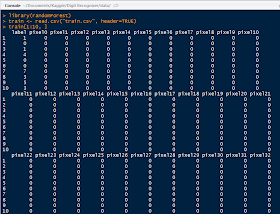 |
| MNIST Training Data |
Before we create the random forest, I would like to show you the images of the digits themselves. The first 10 digits represented by the first 10 rows of written numbers from the training data are shown below.
 |
| Handwritten Numbers |
How did we obtain those PNG images? I formed a 28 x 28 pixel matrix from the training data rows and passed it to the writePNG() function from the png library to output numerical images. Since the values range from 0 to 255, we had to normalize them from 0 to 1 by dividing them by 256.
 |
| Creating a PNG of First Row |
The above code will create a png file for the first row (digit) in the training set. And it will give us this:
 , a one. The below code stacks the rows 1 to 5 on top of the rows 6 through 10.
, a one. The below code stacks the rows 1 to 5 on top of the rows 6 through 10. |
| Creating a Stacked PNG for 10 Digits |
And the image resulting from the above code we saw already, as the first series of handwritten numbers above.
Random Forests
Now that we know how the image was mapped onto the data set, we can use random forests to train and predict the digits in the test set. With the randomForest package loaded, we can create the random forest:
 |
| Creating RandomForest |
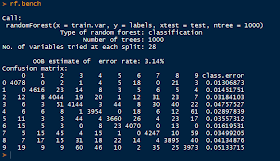 |
| RandomForest |
Above, we have the default output of the random forest, containing the out-of-bag error rate (3.14%), and a confusion matrix informing us how well the random forest classified the 0-9 labels with the actual labels. We see large numbers down the diagonal, but we should not stop there.
Then we can call plot() on rf.bench to visualize the error rates as the number of trees increase:
 |
| plot(rf.bench) |
We see that the aggregate OOB errors decrease and approach 0.0315, as in the output. The OOB error rate describes the error of each bootstrapped sampled tree with 2/3rds of the data and uses the "out of bag" remaining 1/3rd, non-sampled data to obtain a classification using that tree. The error from the classification using that particular tree is the OOB error.
Next we can observe which variables were most important in classifying the correct labels by using the varImpPlot() function.
 |
| Important Pixels |
We can see the most important pixels from the top down- #378, 350, 461, etc. There is another step where we can rerun the random forest using the most important variables only.
Predicting Digits
Lastly, we need to predict the digits of the test set from our random forest. As always, we use the predict() function. However, since we already specified the test data in our randomForest() function, all we need to do is call the proper elements in the object. By using rf.bench$test$predicted we can view the predicted values. The first 15 are down below:
 |
| First 15 Predicted Digits |
After using the write() function to write a csv file, we can submit it to Kaggle (assuming you used the Kaggle data) to obtain the score out of 1 for the proportion of test cases our random forest successfully classifies. We did relatively well at 0.96757.
| Kaggle Submission |
And there we have it, folks! We used random forests to create a classifier for handwritten digits represented by grey-scale values in a pixel matrix. And we successfully were able to classify 96.8% of the test digits.
Stay tuned for predicting more complex images in later posts!
Thanks for reading,
Wayne
@beyondvalence
No comments:
Post a Comment