R: Partial Least Squares Regression, RMSEP, and Components

Hello Readers,

Here we will continue our R regression series and after working with ordinary, and robust regression, we will address partial least squares regression. Using the same chemical descriptors data set, we will predict solubility of compounds with a different approach of looking at the predictors themselves and how they relate to each other. 

In many data sets, the predictors we use could be correlated to the response (what we are looking for) and to each other (not good for variability). If too many predictor variables are correlated to each other, then the variability would render the regression unstable.

One way to correct for predictor correlation is to use PCA or principle component analysis which seeks to find a linear combination of predictors to capture the most variance. The jth principal component (PC) can be written as:

PCj = (aj1 * predictor 1) + (aj2 * predictor 2) + ... + (ajp * predictor p)

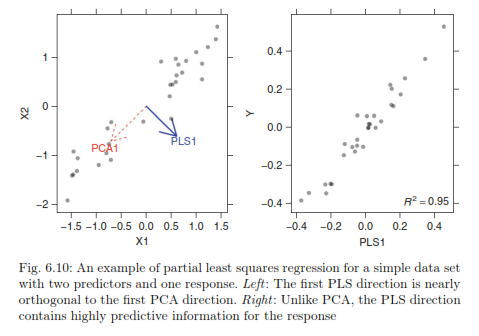
However this method does not always produce a PC that correlates with the response variable as shown below:

From Max Kuhn's Applied Predictive Modeling

Whereas using partial least squares regression, we see that it is correlated with the response variable.

From Max Kuhn's Applied Predictive Modeling

So start R and let us look at partial least squares regression!

Partial Least Squares

PLS regression, like PCA, seeks to find components which maximize the variability of predictors but differs from PCA as PLS requires the components to have maximum correlation with the response. PLS is a supervised procedure whereas PCA is unsupervised.

First we require the following R packages, specifically the pls library:

R Packages

The Solubility data from the AppliedPredictiveModeling package is summarized and transformed in the ordinary regression post.

In the pls library, we will use the plsr() function for partial least squares regression. We specify the response variable as solubility, use all the predictor variables with a ".", and include cross-validation parameter as "CV".

plsr() and Prediction

With the familiar predict() function, use the plsFit list object which contains the predicted values for each component iteration of the PLSR algorithm, with default set at the Dayal and MacGregor kernel algorithm "kernelpls". We predict the first 5 solubility values "solTestXtrans[1:5, ]" using 1 and 2 components "ncomp=1:2". The results are shown below.

Solubility Values for 1 and 2 Components

But how do we know from what number of predictors to choose? Well there are several methods, let us take a look at the summary() output of plsFit, truncated into two parts. We look for component number which adequately explains both predictors and response variances.

The first section displays the root mean squared error of prediction (RMSEP), cross-validation estimate, as well as the adj-CV, which is adjusted for bias. Take note of the dimensions of X and Y of the data towards the top of the output.

pls Summary Part 1

The next section shows the percent of variance explained by components for predictors and response. See how the variance explained rises quickly from 1 component and stabilizes above 10..13 components. That would be a good component range for the pls model.

pls Summary Part 2

Another method is by plotting and locating the lowest Root Mean Standard Error of Prediction (RMSEP).

PLS Prediction Error

There are two methods able to produce the visualization of RMSEP. The first uses the function validationplot() from the pls package which will give us the RMSEP plot for each component iteration in the model. Specify the validation type to be "val.type=RMSEP".

validationplot()

We see from the validation plotting function that there is a sharp decrease in the root mean standard error for the first few numbers of components and then plateaus after about 10. Keep in mind the summary information about the explained variance increments stabilizing around 10.


However we want to find the component number corresponding to lowest point in the RMSEP. Using the RMSEP() function with estimate parameter set to "CV" we can derive the desired value. The plot() will give us the initial graph- see how similar it is to the plot obtained from validationplot(). (They should be the same.)

RMSEP() and plot()

To calculate the lowest RMSEP, we use the which.min() function, which returns the index of the lowest value. The minimum value is found at 10 components and we add a point to the plot using the points() function such that the x and y values are: (component number, minimum RMSEP value).

Finding Lowest RMSEP

The plot with the added locating point in red is shown below.

RMSEP() with points()

Using the training data, we can plot the predicted solubilities from the training set to the actual solubilities, using another plot() function:

plot(plsFit, ncomp=10, asp=1, line=True)

Checking Training Predictions

From the above plot, we see that the points mainly lie along the line. This is expected because the data is from the same training set used to create the plsr model.

Predicted Solubilities

Now that we have an optimal component number (10), we can go ahead and use the plsr model to predict new solubility values for test predictor data. Again we use the predict() function and specify the test data (solTestXtrans) and the number of components (ncomp=10).

Predicting Solubility from Test Data

Then we plot the observed ('test' data with actual values,  lucky us) and the predicted values together with a line, determining how close the values are.

And the plot does not look too bad, with no indication of anomalies.

Evaluation of plsr Model

Because we have the observed solubility values for the 'test' data we can evaluate how well the model performed. However in the usual circumstances, we would not know the actual values, hence what we are doing- predicting values from the test predictor data.

Using the observed values in solTestY and the predicted values in pls.pred2[,1,1], we can use the defaultSummary() function to obtain the RMSE and Rsquared, as shown below.

Evaluation

From the output, we see that the RMSE is around 0.7366, and the Rsquared is approximately 0.8744, explaining 87% of the test data variance.


And there we have it, folks! This (lengthy) post covered partial least squares regression in R, starting with fitting a model and interpreting the summary to plotting the RMSEP and finding the number of components to use. Then we predicted solubilities from the the test data with the plsr model we fitted to the training data.

Check back for more posts on predictive modeling! Happy programming guys!


Thanks for reading,

Wayne
@beyondvalence