Cluster Analysis: Using K-Means in R

Hello Readers,



Hope you guys are having a wonderful holiday! (I am.) Today in this post we will cover the k-means clustering technique in R.

We will use the familiar iris data set available in R.


Let us get started!

K-Means Clustering

Start by loading the cluster package by library(cluster) in R. The first and very important step in k-means clustering occurs when choosing the number of final clusters (k). 

Therefore the k-means clustering process begins with an educated 'guess' of the number of clusters. With the k number of clusters, R selects k observations in the data to serve as cluster centers. Then the Euclidean distance is calculated from observations to the cluster centers, and the observations are placed in the cluster to which they are closest.

Then the center of each cluster is recalculated and the Euclidean distance is taken for each observation and the new cluster center. R checks every observation to see if it is closer to another cluster center and reassigns it if it is closer to another cluster. The process of center cluster recalculation and observation distance checking is repeated until observations stay in the same cluster.

The kmeans() function requires the choosing k observations as the centers of the clusters.

Before clustering, remove the species column from the iris data set to retain the numerical values only.

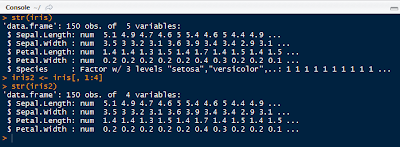Iris2 Data Set Without Species

Now use the kmeans() function on iris2 with 3 centers, or number of clusters, as shown below with the output.

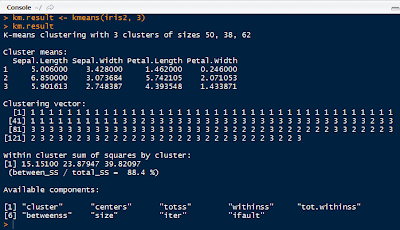K-Means Result

Note that the output includes the size of each cluster (50, 38, 62), the means of each variable in each cluster, the vector of the cluster number, the withinss for each cluster, and the components of the km.result object.

kmeans() seeks to minimize the withinss for each cluster, which is the sum of of squared error (SSE) or scatter. It is calculated by taking the sum of the squares of the distances between the observations and centroid of each cluster.

To see how well the k-means clustering performed, we can create a table with the actual species of iris and the cluster numbers:

Species and Cluster Comparison

As we can see, the clustering successfully clustered all the setosa species, but had difficulty with virginica (14 off) and versicolor (2 off). To quantify the agreement we can use the the library(flexclust) package, as shown below:

Adjusted Rank Index

An agreement of 0.73 is not too bad, as it ranges from -1 (no agreement) to 1 (perfect agreement). We have a 0.73 agreement between the iris species and cluster solution.

Plotting Clusters

Next we can visualize the clusters and their centers we constructed, with the code below:

Plotting Code

And that yields the visual below. Note that the three diamonds are the cluster centers in black, green and red.

Iris Clusters Plot

The model looks OK, except for a few red cluster points close to the green center, possibly miss classification of the virginica and versicolor species, because setosa was completely categorized properly. As we can see, the clustering is not perfect, hence an agreement score of 0.73.


In the next Cluster Analysis post I will discuss finding a suitable k to begin the k-means analysis. In this case, we knew we had 3 species to begin, so it was easy to plug in the k. However, we will look at the within sum of squares and sets of criteria to see what k we will use for a data set on wine. Stay tuned!


Thanks for reading,


Wayne
@beyondvalence