Cluster Analysis: Choosing Optimal Cluster Number for K-Means Analysis in R

Hello Readers,

Last time in Cluster Analysis, we discussed clustering using the k-means method on the familiary iris data set. We had know how many clusters to input for the k argument in kmeans() due to the species number. 

Here we shall explore how to obtain a proper k through the analysis of a plot of within-groups sum of squares against the number of clusters. Also, the NbClust package can be a useful guide as well.


We will use the wine data set in the rattle package. Open R and load the rattle package and let us get started!

The Wine Data

Call str() on wine and study the components of the wine1 data set after taking out the first variable with wine[-1].

Wine1 Data

We see that wine1 is a collection of 178 observations with 1 variables- 13 numeric and integer variables. The variable we removed is a factor describing the type of wine. Try not to peek at the original data!

To see what the data look like, we could call pairs() on wine1 but good luck with analyzing that plot! Instead call head() on wine1 to get an idea (first 6 observations) of the set.

First 6 Observations in Wine1

Now we are acquainted with the data, we can go ahead a determine the best initial k value to use in k-means clustering.

Plotting WithinSS by Cluster Size

Like we mentioned in the previous post, the within group sum of squares (errors) shows how the points deviate about their cluster centroids. So by creating a plot with the within group sum of squares for each k value, we can see where the optimal k value lies. This will use the 'elbow method' to spot the point at which the within group sum of squares stops declining as quickly to determine a starting k value.

We do this by writing a function in R. I will call it wssplot(). The function will loop through fifteen k values to ensure that most reasonable k values will be considered. The first value for wss is assigned the sum of squares for k=1 by canceling out the n-1 term in the sum of the variances. Then the for loop starts at k=2 and loops to k=15, assigning the within sum of squares from the kmeans$withinss component for each iteration.

The wssplot also creates a plot of the within groups sum of squares.

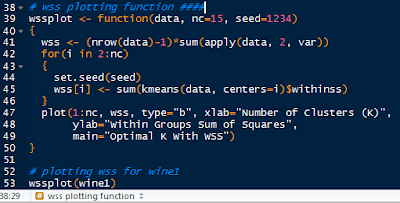wssplot Code

This yields the within groups sum of squares plot for each k value:

Within Group Sum of Squares by Cluster Number

We see that the 'elbow' where the sum of squares stops decreasing drastically is around 3 clusters, then the decrease tapers off. This is our k value!

The NbClust is a package dedicated to finding the number of clusters by examining 30 various indices. We set the minimum number of clusters at 2 and the maximum at 15.

NbClust Code

The table will yield the clusters chosen by the criteria. Note not all of the criteria could be used. As we can see, 3 clusters had the overwhelming majority.

Clusters Chosen by Criteria

These are just some ways in which we can obtain the optimal k value before starting the kmeans clustering. The kmeans output is shown below in aggregate(), with k = 3.

Variable Averages in Each Cluster

We can check how well the kmeans clusters =3 clustered the data by using the flexclust package. See how well the clustering was for wine types 2 and 3? Not very well with a low index of 0.371.

Wine Table and Index

In following posts, we will cover hierarchical clustering. So stay tuned!



Thanks for reading,


Wayne
@beyondvalence
LinkedIn
(link)