Ukraine Crisis and Palladium Prices

Hello Readers,


So far we have dealt with time series (and other data) on this blog with raw R plot outputs, predicted trends, and time series decomposition. This post will take an aesthetic turn to data presentation, and transforming a graph into a graphic. A previous post turned #Crimea tweets into a word cloud.

Resulting Graphic

We will focus on Crimea, and element palladium, Pd (atomic number 46), where the rare metal constitutes parts of catalytic converters, electronics, jewelry, dentistry, and fuel cells . Why palladium and Crimea together? Well, in late January of 2014, nearly 70,000 miners in South Africa called a strike, stopping 40% of world production of palladium. Although talks in late April appear to have solved the issues, the strikes are still on, as of this writing. With Russia producing 44% of the world's palladium supply, Russia and South African control 84% of the world's palladium production.

Catalytic Converter

As sanctions flew back and forth due to the Ukraine Crisis, the supply of palladium from Russia was considered at risk. Pro-Russian forces entered the Crimean peninsula in February, days after Russia refused to acknowledge the Yatsenyuk Government post Ukrainian Revolution. After a majority in the referendum in Crimea voted to join Russia, the United States and EU denounced Russia as Putin signed a treaty of accession with Crimea and Sevastopol. Then several eastern cities in Ukraine came under occupation by pro-Russian forces/demonstrators, who seized government buildings. 

Click here for Ukraine Crisis in Maps by The New York Times

Even with the Ukraine Agreement on April 17th, temporarily stopping hostilities between Ukraine and Russia, tensions are still rising as politicians in Kiev seek to oust militants from their eastern cities. The deputy prime minister of Ukraine, Vitaliy Yarema, said "the active phase of the anti-terrorist operation continues" after the Easter holiday (April 26-27th), despite 40,000 Russian troops massing at the Russian-Ukrainian border, conducting military drills.

The United States has responded by sending troops to Poland, Lithuania, Latvia, and Estonia, after NATO increased their presence in eastern Europe. EU and NATO countries have resorted to sending troops in response to Russian troop movement, and international sanctions on Russia had little effect on their military actions surrounding Ukraine.

While Vladimir Putin acts undeterred by the wide economic sanctions, and of top Russian officials, troop movement on both sides will only escalate. That not only endangers palladium production (the point of the post), but also risks the lives of Ukrainians and the future of eastern Europe.

Palladium Data

I obtained the palladium data from Quandl, a site that hosts data sets. The palladium data source is from John Matthey's Precious Metals Marketing. You can download the data by clicking the red download button and selecting the file type (I picked CSV).

Quandl- Palladium Prices

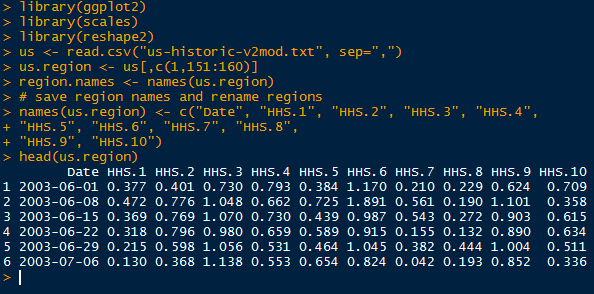
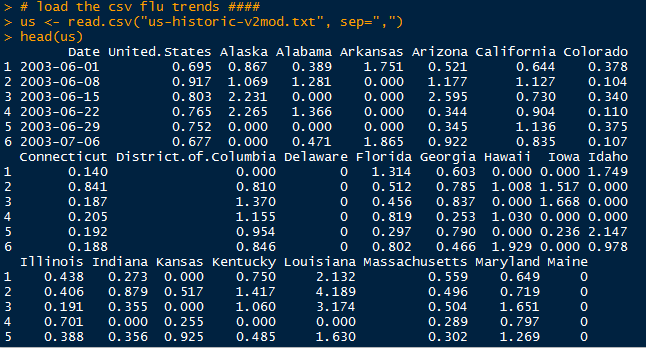
Open R, and read the CSV file with a header. Make sure your working directory is set where the data set is saved, and use the head() function to get an idea of what the data set contains.

Snapshot of Palladium Data

We see a date column with the format of "year-month-day", and the morning and afternoon prices in Hong Kong and New York, and only the morning price from London. We need to format the date column into a date type using as.Date(). Call str() to verify the type of the date column. Looking below, the date column is now in the date format.

Date Format

We will use the morning prices from Hong Kong ($Hong.Kong.8.30) because it has the most consistent, recent data out of the 5 price variables. For the recent date range, we aim for 2010 to present to capture the rise in palladium prices in 2011 in addition to the prices in late April 2014. After some exploring, we discover the starting index at row 1080.

Subset and Fix Value Typo

After we create the new subset, of the values from 2010 onward for the date and morning HK values, we discover the price range is slightly odd. There is a rather low anomaly price of 72. Using which.min() we locate the low price index at 131. To verify 72 is (in)correct, we look at the other variable locations at row 131, and realize that 72 was not the likely starting price. We impute a value of 723 at row 131 based on prices from other locations.

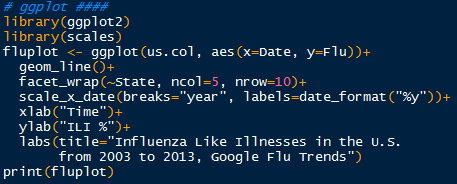
Now we can plot the palladium price get an idea of the data trend (and to see if it matches vaguely with the plot on Quandl). Add some color, axis labels, and title to the plot.

Plotting Palladium

We see the result below. Looks good, but this 'good' does not represent publishable material. This is simply raw R plot output.

Raw R Plot Output

Since this post is about turning a graph into a graphic, I made a few modifications to the R plot in Adobe Illustrator. First I used the direct selection tool to delete the plot borders, and to move the title, axis labels, and create the dashed lines as enhanced tick marks. Then I utilized the type tool to add text to highlight specific events on the time series, and created a sub-title explaining the graphic.

As a result of refining the plot through Illustrator, we see an improved visual with more pertinent information about South African, Ukraine, Russia, and palladium prices. The view can observe the events from the labels, and see the rise in palladium prices in response. However, this is not mean direct causation, but logically the effect of strikes/sanctions with production control and rising scarcity/prices makes sense. We want the visualization to invoke thought, and raise questions about the mechanisms behind the palladium price fluctuations. (Hopefully we will not encounter WWIII- and Putin is not shy about brinkmanship).

Stay tuned for more R analytics posts, and keep an eye out for additional visualization posts!


Thanks for reading,

Wayne
@beyondvalence
LinkedIn

Visualizing Google Flu Trends Part 2

Hello Readers,


This post continues the visualization of flu trends from Google. Last time we plotted the flu time series for 50 states from 2003 to 2013. Here we will visualize the flu trends through 10 regions set by the Department of Health and Human Services (HHS). We shall enlist the aid of the melt() function from the reshape2 library.

So load ggplot2, scales, and reshape2 in R, and let us get started!

10 HHS Regions

Recall from the previous flu trends post, that the data was obtained from the Google Flu Trends site. The CSV file includes influenza like illness percentages from doctor visits for 50 states, District of Columbia, 97 major cities and 10 HHS regions. Since we already visualized the 50 states, we turn to the 10 HHS regions.

Flu Data in U.S. Regions

Last time we used a custom function to pull data from each column into 1 column. Then we bound a respective column with the 50 state names. Likewise, the date values were repeated 50 times, for a total of 3 columns. The original saved region names are shown below, along with the states they contain.

Original Region Names with States

However, there is (almost always) a more efficient way. In the reshape2 library, there exists a function which will arrange all the desired values into one column from multiple columns. Simply specify which variable to keep constant, and the melt() function will create variable column identifying the value column.

Melted Flu Trends in U.S. Regions

Now we are ready to visualize the flu data by region.

Creating the Visuals

Using ggplot(), we specify the Date on the x axis, and the value on the y axis. Furthermore, we use facet_wrap() to stratify by variable (HHS regions) into 10 plots, 2 columns of 5.

Plot Code

This yields the plot below:

Like we confirmed in the last post, here we also see dramatic peaks in all regions from 2003-2004, and 2009-2010. HHS region 6, which includes Arkansas, Louisiana, New Mexico, Oklahoma, and Texas has higher consistent peaks than the other 9 regions.

We could have plotted the 10 regions in one plot, however, the lines would be difficult to differentiate:

Plot Code

Looking at the plot below, we observe multiple colors, each a region, and peaks in each region occur within a similar time window. All the lines in one plot makes it difficult to evaluate each time series individually, but allows relative comparison between regions.

Again we encounter an alternative method to writing a custom function. The melt() function rearranges a data.frame for us. And that concludes this post. Stay tuned for more data analysis!


Thanks for reading,

Wayne
@beyondvalence
LinkedIn

Visualizing Google Flu Trends in R

Hello Readers,


Today we will visualize influenza trends in the United States, captured from Google.org Flu Trends. By combining flu symptom search queries with CDC flu data, Google was able to estimate how many of those searching for flu symptoms actually had the flu, or had influenza like illness (ILI). Locations are determined from IP addresses via their server logs.

Above is a plot of the average percentage of influenza like illness among the 50 states. We will look at weekly time series data for each 50 states from Google Flu Trends from June of 2003 to October of 2013. Click here for the text file. 

Load the ggplot2, scales libraries in R, and let us get started.

Flu Data

After reading in the "us-historic-v2mod.txt" as a CSV file, we call head() and check what we have:

Raw Data

Our data set contains 541 observations in time with 160 variables of U.S. average, states, cities, and regions. We isolate the state variables along with the date into a new data.frame, and convert the Date column into a "year-month-day" date format.

New Data.Frame with States

Because we want to use ggplot() to display the flu trend for each of the 50 states, we have to create a new data.frame will all flu trend data in one column and the state in another. Essentially, we have to row bind all data from 50 states together.

Data.Frame Conversion

After we generated a Date, Flu, and State columns, we can column bind them together. However, make sure to use cbind.data.frame() instead of regular cbind() to preserve the date format.

Converted Data.Frame

Now we are ready for plotting the flu data.

Visualization of the Flu Data

Earlier I mentioned to load the ggplot2 and scales libraries. Next, we use the ggplot() function to begin our plot. The key to plotting 50 trends lies in the facet_wrap() function, where we stratify or 'facet' the State variable, and specify the number of columns and rows to display. Note that the State variable is a factor. The scale_x_date() function allows us to customize the x axis display to show the last 2 digits of every year ("%y").

Plot Code

Pass the fluplot through print() and we obtain the plot below:

That is quite a lot of data to process visually at one time. After scanning the plot, we observe that the fluctuation in some states, such as Wyoming, Utah, or Florida, are not as prominent as other states- New Mexico, Arkansas, or Oklahoma. Some of these differences could be attributed to state population. 

However, almost every state at the start of a new year has a peak or increase in influenza like illness. The majority of states have higher peaks in 2003-2004, and 2009-2010. Recall the H1N1 incident from 2009-2010, where influenza of swine origin with novel viral genes threatened a pandemic. Due to the vigilance of the CDC, state and local health departments, hospitals, and healthcare personnel, quick vaccine creation and high vaccination levels prevented H1N1 from reaching pandemic distribution.

Yes, these  flu data are time series, so we will be able to decompose them and predict future ILI percentages! So stay tuned for more posts!


Thanks for reading,

Wayne
@beyondvalence
LinkedIn

How Fast is Fast? Comparing U.S. and South Korea Broadband Speeds in R

Hello Readers,


You might have heard about Google Fiber, where you browse and stream in the world of blindingly fast internet speed. How fast exactly? 100 times as fast, at 1,000 mbits/s (megabits per second). The rest of us in the United States have to trudge along with an average of 20 mbits/s while downloading, where actual speeds lag in around ~8 mbits/s. Such is the power of the clauses like "speeds up to __".

Unfortunately Google Fiber is only available in select cities (Kansas City, Austin TX, and Provo UT). So if you do not live there or any of these places, you probably will still be streaming Netflix and YouTube at average speed. Bummer. Here is a YouTube video demonstrating Google fiber speeds.

Internationally, the United States is beginning to lag behind other countries in broadband speed (download and upload). Take South Korea for instance. Entering into this millennium, South Korea has built significant networking infrastructure, and South Korean brands such as Samsung and LG have permeated the world electronic stage with high quality products. What Japan accomplished with innovating cars, right now South Korea is doing with electronics. And you guessed it, they also upgraded their broadband infrastructure as their economy focused on high tech in the 1990s. Their download and upload speeds are more than twice that of US counterparts (we generate the below plot in the post). 

S.K. Download Speeds in 2009 > U.S. Download Speeds in 2014

Also, two of South Korea's largest mobile carriers, SK Telecom and LG Uplus Corp, are rolling out a new LTE broadband network in 2014 at 300 megabits per second. Compare that speed to 8 megabits per second here in the U.S. There are many factors involved to make this possible in South Korea, such as high population density of 1,200 people per square mile, and government regulation to bolster competition among service providers. In the U.S., providers have their own closed-network system, so by switching to/from Comcast or Verizon, you would have to install new cables. This infrastructure dilemma acts as a cost barrier for new companies looking to enter into the broadband market.

Enough of the Fiber talk. We are here to discuss average internet broadband speeds for average people. And just because our internet is slower here in the U.S., does not mean that it does not work. Lucky us, there is open data available at Data Market. Let us start R and crunch the data!

Broadband Data

Start here for the exact data set from Data Market. This data is provided by Ookla, an internet metrics company. You most likely have used their speed test utility to measure your internet speed. The data set has many countries from which to select the download and upload speeds including the World average speed in kilobits per second. Make sure the United States and South Korea variables are selected with download and upload speeds before clicking the Export tab and downloading the CSV file.

Data Market- Broadband Speeds CSV

Now that we have downloaded the CSV file, we can import it into R:

Reading in the Broadband CSV Data

Note the columns and their data. There are 5 columns designating the year-month, South Korean download speed, South Korean upload speed, U.S. download speed, and U.S. upload speed, all in kilobits per second. We will be splitting the the last four into individual time series and appending them to a list due to their different lengths (South Korea has less data points). 

Remember to remove the last row in all columns, since it contains just a descriptor of the variables and null values. The creation will result in 4 time series: download and upload speeds for the U.S., and download and upload speeds for South Korea. Take notice that we divide each time series by 1000 to obtain megabits per second from kilobits per second.

Creating Time Series Data.frames and a List Class

The bb (broadband) list allows us to use a shorter input method, and aggregates all the time series into one list object. We could not create a data.frame with all four time series because the South Korea and U.S. series have different number of data points. South Korea data start at September 2008, whereas U.S. data start in January 2008. The bb list contents are shown below:

Time Series in List Contents

Check that the time series are in megabits by comparing the values. They should be three orders of magnitude less.

Plotting Broadband Speeds

Since we have two countries with two time series each, we will prudently use color coding for visual purposes. First we plot the download speed for South Korea in dark green using plot(), making sure to specify custom y and x axis to fit the data for U.S. as well. Next we add the remaining three time series with lines() with upload speed for South Korea in green, and the download and upload speeds for the U.S. in dark orange and orange, respectively.

Broadband Time Series Plot Code

Lastly we add a legend with the label and colors to yield our plot below:

Broadband Plot

And look at those colors! We can observe the South Korean green lines after mid 2011 are much higher than the orange yellow lines of the U.S. broadband speeds. In fact, we can see that download speeds in South Korea in 2009 were higher than our download speeds in the U.S. now in 2014! 

The Future of Broadband?

Of course we would want to know the forecasts of the time series. With our current technologies, how fast would our broadband speeds be in 2 years? Specifically, we want to ballpark our download speeds in the U.S. compared to South Korea. In previous time series posts, we used regression and ARIMA methods to forecast future values for wheat production and Amazon stock prices respectively. To create a prediction, or forecast, we will turn to exponential smoothing for these broadband data.

Exponential smoothing estimates the next time series value using the weighted sums of the past observations. Naturally we want to weight more recent observations more than previous observations. We can use 'a' to set the weight 'lamba':

lambda = a(1-a)^i, where 0 < a < 1
such that xt = a*xt + a(1-a)*xt-1 + a(1-a)^2 * xt-2 + ...

This procedure is called the Holt-Winters procedure, which in R manifests as the HoltWinters() function. This function includes two other smoothing parameters B for trend, and gamma for seasonal variation. In our case, we would simply specify the data and R will use determine the parameters by minimizing the mean squared prediction error, one step at a time.

Let us consider the exponential smoothing over the download speeds of the U.S. and South Korea. The U.S. output is shown below:

Holt-Winters Exponential Smoothing

We can see the HoltWinters() function determined the three parameters, alpha, beta, and gamma. Next we overlay the fitted values from the HoltWinters() function to the real download speed time series to visualize how they approximate the actual values. The plot code is shown below, with different line colors for visual contrast:

Holt-Winters Plot Code

The resulting plot is displayed below:

Okay, the Holt-Winters procedure did a good job of approximating the the observed time series values, as seen by the red and yellow lines above for estimated U.S. and South Korea download speeds.

Now that we have confirmed the model, we will go ahead and predict the next 2 years of broadband download speeds using the predict() function passing through the Holt-Winters objects. The predicted values are shown below:

Predicted 2 Years Values from Holt-Winters

We can see the U.S. predicted download speeds approach 28 mbits/s by 2016. For South Korea in 2016, the estimated download speed exceeds 60 mbits/s. Next we plot these predicted values with the download speeds time series with a dashed line type to differentiate the observed and predicted values with lty=2.

Plotting Predicted 2 Year Values

The prediction plot is depicted below.

Observe the U.S. download speeds with 2 year forecast in orange, and the South Korea download speeds in green. Note the forecasts as dashed lines. We see that the exponential smoothing predicted increases in U.S. and South Korea download speeds, with South Korea download speeds over 60 mbits/s and 28 mbits/s in the U.S.

In case you were curious, I also predicted the future upload speeds 2 years ahead to 2016 as well. U.S. upload speeds predicted by the Holt-Winters procedure barely exceeds 5 mbits/s, while upload speeds in South Korea rises above 55 mbits/s. Both predicted download and upload speeds in South Korea in 2016 are well beyond the broadband speeds in the U.S. The upload speeds plot is shown below:

Hopefully this post gives you guys a better idea of the state of broadband speeds now and after here in the U.S., and what could be possible, namely in South Korea. It is humbling to reiterate again that download speeds in the U.S. now in 2014 have not yet exceeded South Korean download speeds back in 2009. 

We would have to keep an eye out on this Comcast merger with Time Warner Cable. Merged, Comcast would control 40% of broadband market and have 30 million TV subscribers. And if New York allows it, I suspect lukewarm increases in broadband speeds, if at all. Google Fiber, where are you?

Stay tuned for more R posts!


Thanks for reading,

Wayne
@beyondvalence
LinkedIn

Up, Up, And Away: Amazon Stock Prices in R

Hello Readers,

Today we turn to the world of finance as we look into stock prices, specifically that of Amazon, Inc (AMZN). AMZN has been traded on the NASDAQ stock exchange since their IPO on May 15th, 1997  at 18.00 per share. Nowadays in 2014, AMZN trades around 369 dollars a share. Quite a long ways from a simple book selling company in Jeff Bezo's garage. I am sure Jeff Bezos is smiling. A lot.

Jeff Bezos, Founder and CEO/Chairman/President of Amazon

At the Yahoo Finance site, we can download AMZN stock price data, such as the opening price, the high and low of the day, closing price, and the volume (number of stocks bought and sold). Check the beginning date is March 3, 2008, the end date is March 12, 2014 (when I retrieved the data), and prices are set to monthly. Then at the bottom of the chart, there is a 'Download to Spreadsheet' CSV link (or just click the link).

Download AMZN Prices from Yahoo Finance

Now that we have the stock prices data, let us start number crunching to predict future Amazon stock prices in R.

AMZN in R

We need to import the CSV file into R. Locate the AMZN CSV file in your computer directory and write a read.csv() function pointing along the directory, making sure header=True. We will be using the closing prices.

Reading in CSV and AMZN Data

We see from the first six rows in amzn, that the closing prices are in 5th column, and the prices are ordered from most recent to previous prices. When creating the time series, we need to reverse the 5th column, and specify the starting month and year with start=c(2008, 3). There are 12 monthly prices in a year so freq=12.

Creating AMZN Time Series and Data.frame

In addition to the single time series, we can manipulate the data by taking the log of the values and placing both into an accessible data.frame.

Next we plot the AMZN stock prices to get an idea of any trends in the prices over the 6 years.

Plotting Both AMZN and log AMZN Prices

Below we have the two plots, the AMZN stock price and the log of the AMZN stock price. We can see the obvious rise over the 6 years from 71.3 in March 2008 to 370.64 in March of 2014.

Observe the same upwards trend for the log of the stock prices. Note that fluctuations at lower values  (around 2009) tend to produce greater effect when log transformed, since the values are the exponents of base e.

Decomposition

There is a function, stl(), which decomposes the amazon time series into seasonal, trend, and remainder components. stl() finds the seasonal component through loess smoothing (or taking the mean if s.window="periodic"). The seasonal component is removed from the data and the remainder is smoothed to find the trend. The residual component is calculated from seasonal plus trend fit residuals. Use the stl() function to decompose the closing prices in amazon, and plot the result.

amazon Decomposition

See how variable the seasonal component is through the extreme values ranging from -5 to 10. There are also definitive peaks and valleys at specific times during the year. For example, in the 4th quarter (Q4- October, November, and December) this is a dramatic rise and fall in price by about 15 points.

Overall, the trend shown above depicts the expected upwards trend in stock price, besides the prices from 2008 into 2009, coinciding with the great financial collapse. Next we will use this output to forecast the price of AMZN stock in 2 years- March 2016.

Forecasting with stl()

Load the forecast package with the library() function. It enables us to forecast different time series models and linear models with the forecast() function. We specify our decomposed time series, amazon.stl, and determine our prediction method as "arima". Next we want to predict 24 periods into the future (or 24 months- 2 years), with a 95% confidence interval specified with level=95. Then we visualize our results by passing our forecast object through plot().

stl() ARIMA Forecasting AMZN

We see the resulting (wonderful) plot below. Observe the forecast prices modeled and determined by auto.arima as the blue line, shadowed by the 95% confidence interval in grey. (ARIMA was cover in this post.) The model forecasts a likely increase of the AMZN stock price over 400 through year 2016.

The forecast values for AMZN through 2016 are shown below. The forecast for AMZN in March 2016 is 470.42, with a 95% confidence interval of the actual value lying between 333.96 and 606.88.

Forecast AMZN Values

From that forecast, I would buy some AMZN stock! Especially after Amazon announced on March 14th that they would raise Amazon Prime membership by $20 to $99 a year for free two-day shipping, video streaming, and other features. Many analysts concluded this move would increase profits by millions and AMZN stock rose 1% (about 3.5 points). I am sure Jeff Bezos is smiling even more.

OK folks, hopefully now you have a better understanding of decomposition and forecasting time series! Check back for more analytic posts!


Thanks for reading,

Wayne
@beyondvalence