R: Comparing Multiple and Neural Network Regression

Hello Readers,


Today we have a special competition between linear and neural network regression. Which will model diamond data best? Load the ggplot2, RSNNS, MASS, and caret packages, and let us turn R into a diamond expert. While the statistical battle begins, we can learn how diamonds are priced.


READY TO RUMBLE: Diamond Data

Here we will compare and evaluate the results from multiple regression and a neural network on the diamonds data set from the ggplot2 package in R. Consisting of 53,940 observations with 10 variables, diamonds contains data on the carat, cut, color, clarity, price, and diamond dimensions. These variables have a particular effect on price, and we would like to see if they can predict the price of various diamonds.

diamonds Data

The cut, color, and clarity variables are factors, and must be treated as dummy variables in multiple and neural network regressions. Let us start with multiple regression.

TEAM: Multiple Regression

First we ready TEAM: Multiple Regression by sampling the rows to randomize the observations, and then create a sample index of 0's and 1's to separate the training and test sets. Note that the depth and table columns (5, 6) are removed because they are linear combinations of the dimensions, x, y, and z. See that the observations in the training and test sets approximate 70% and 30% of the total observations, from which we sampled and set the probabilities.

Train and Test Sets

Now we move into the next stage with multiple regression via the train() function from the caret library, instead of the regular lm() function. We specify the predictors, the response variable (price), the "lm" method, and the cross validation resampling method.

Regression

When we call the train(ed) object, we can see the attributes of the training set, resampling, sample sizes, and the results. Note the root mean square error value of 1150. Will that be low enough to take down heavy weight TEAM: Neural Network? Below we visualize the training diamond prices and the predicted prices with ggplot().

Plotting Training and Predicted Prices

We see from the axis, the predicted prices have some high values compared to the actual prices. Also, there are predicted prices below 0, which cannot be possible in the observed, which will set TEAM: Multiple Regression back a few points.

Next we use ggplot() again to visualize the predicted and observed diamond prices from the test data, which did not train the linear regression model.

Plotting Predicted and Observed from Test Set

Similar to the training prices plot, we see here in the test prices that the model over predicts larger values and also predicted negative price values. In order for TEAM: Multiple Regression to win, TEAM: Neural Network has to have more wild prediction values.

Lastly, we calculate the root mean square error, by taking the mean of the squared difference between the predicted and observed diamond prices. The resulting RMSE is 1110.843, similar to the RMSE of the training set.

Linear Regression RMSE, Test Set

Below is a detailed output of the model summary, with the coefficients and residuals. Observe how carat is the best predictor, with the highest t value at 191.7, with every increase in 1 carat holding all other variables equal, results in a 10,873 dollar increase in value. As we look at the factor variables, we do not see a reliable increase in coefficients with increases in level value.

Summary Output, Linear Regression

Now we move on to the neural network regression.

TEAM: Neural Network

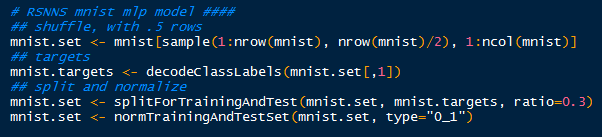
TEAM: Neural Network must ready itself as well. Because neural networks operate in terms of 0 to 1, or -1 to 1, we must first normalize the price variable to 0 to 1, making the lowest value 0 and the highest value 1. We accomplished this using the normalizeData() function. Save the price output in order to revert the normalization after training the data. Also, we take the factor variables and turn them into numeric labels using toNumericClassLabels(). Below we see the normalized prices before they are split into a training and test set with splitForTrainingAndTest() function.

Numeric Labels, Normalized Prices, and Data Splitting

Now TEAM: Neural Network are ready for the multi-layer perceptron (MLP) regression. We define the training inputs (predictor variables) and targets (prices), the size of the layer (5), the incremented learning parameter (0.1), the max iterations (100 epochs), and also the test input/targets.

Multi-Layer Perceptron Regression

If you spectators have dealt with mlp() before, you know the summary output can be quite lenghty, so it is omitted (we dislike commercials too). We move to the visual description of the MLP model with the iterative sum of square error for the training and test sets. Additionally, we plot the regression error (predicted vs observed) for the training and test prices.

Plotting Model Summaries

Time for TEAM: Neural Network so show off its statistical muscles! First up, we have the iterative sum of square error for each epoch, noting that we specified a maximum of 100 in the MLP model. We see an immediate drop in the SSE with the first few iterations, with the SSE leveling out around 50. The test SSE, in red, fluctuations just above 50 as well. Since the SSE began to plateau, the model fit well but not too well, since we want to avoid over fitting the model. So 100 iterations was a good choice.

Second, we observe the regression plot with the fitted (predicted) and target (observed) prices from the training set. The prices fit reasonably well, and we see the red model regression line close to the black (y=x) optimal line. Note that some middle prices were over predicted by the model, and there were no negative prices, unlike the linear regression model.

Third, we look at the predicted and observed prices from the test set. Again the red regression line approximates the optimal black line, and more price values were over predicted by the model. Again, there are no negative predicted prices, a good sign.

Now we calculate the RMSE for the training set, which we get 692.5155. This looks promising for TEAM: Neural Network!

Calculating RMSE for MLP Training Set

Naturally we want to calculate the RMSE for the test set, but note that in the real world, we would not have the luxury of knowing the real test values. We arrive at 679.5265.

Calculating RMSE for MLP Test Set

Which model was better in predicting the diamond price? The linear regression model with 10 fold cross validation, or the multi-layer perceptron model with 5 nodes run to 100 iterations? Who won the rumble?

RUMBLE RESULTS

From calculating the two RMSE's from the training and test sets for the two TEAMS, we wrap them in a list. We named the TEAM: Multiple Regression as linear, and the TEAM: Neural Network regression as neural.

Creating RMSE List

Below we can evaluate the models from their RMSE values. 

All RMSE Values

Looking at the training RMSE first, we see a clear difference as the linear RMSE was 66% larger than the neural RMSE, at 1,152.393 versus 692.5155. Peeking into the test sets, we have a similar 63% larger linear RMSE than the neural RMSE, with 1,110.843 and  679.5265 respectively. TEAM: Neural Network begins to gain the upper hand in the evaluation round.

One important difference between the two models was the range of the predictions. Recall from both training and test plots that the linear regression model predicted negative price values, whereas the MLP model predicted only positive prices. This is a devastating blow to TEAM: Multiple Regression. Also, the over prediction of prices existed in both models, however the linear regression model over predicted those middle values higher the anticipated maximum price values.

Sometimes the simple models are optimal, and other times more complicated models are better. This time, the neural network model prevailed in predicting diamond prices.

Winner: TEAM: Neural Network

Stay tuned for more analysis, and more rumbles. TEAM: Multiple Regression wants a rematch!

Thanks for reading,

Wayne
@beyondvalence
LinkedIn
rumble

Neural Network Prediction of Handwritten Digits (MNIST) in R

Hello Readers,


Today we will classify handwritten digits from the MNIST database with a neural network. Previously we used random forests to categorize the digits. Let us see how the neural network model compares to the random forest model. Below are 10 rendered sample digit images from the MNIST 28 x 28 pixel data.

Instead of using neuralnet as in the previous neural network post, we will be using the more versatile neural network package, RSNNS. Lastly, we evaluate the model with confusion matrices, an iterative error plot, regression error plot, and ROC curve plots.

MNIST Data

Ah, we return to the famous MNIST handwritten digits data set (available here). Each digit is represented by pixels 28 in width and 28 in height, for a total of 784 pixels. The pixels measure the darkness in grey scale from blank white 0 to 255 being black. With a label denoting which numeric from 0 to 9 the pixels describe, there are 785 variables. It is quite a large data set considering the 785 variables from 42,000 rows of image data.

I made it easier to manage, and faster to model by sampling 21,000 rows from the data set (half). Later, I might let the model run overnight for the entire 42,000 rows, from which I will update the results in this post. Recall that the random forest model took over 3 hours to crunch in R.

After I randomly sampled 21,000 rows, I began to create the targets inputs for which to train the input data. Afterwards with splitForTrainingAndTest(), the targets and inputs are separated into- you guessed it, training and test data according to ratio I set at 0.3. Because the grey scale values proceed from 0 to 255, I normalized them from 0 to 1, which is easier for the neural model.

Tidying Up the Data

Now the data is ready for the neural network training with the mlp() function. It creates and trains a multi-layered perceptron- our neural network. 

Training the Neural Network

And after some time, it will complete and we can see the results! Also evaluate and predict the test data with the model.

Results and Graphs

With 784 variables, calling summary() on the model would inundate the R console, since it would print the inputs, weights, connects, etc. So we need to describe the model in different ways. 

 Confusion Matrix
How about looking at some numbers? Specifically, at the confusion matrix of the results for the training and test data using the function confusionMatrix(). (Note that R will mask the confusionMatrix() function from the caret package if you load RSNNS after caret- access it using caret::confusionMatrix()).   

We pass the targets for the training data, and the fitted values (predicted) from the model to compare how the model classified the targets with the actual targets. Also, I changed the dimension names to 0:9 to mirror the target numerals they represent.

Creating Training and Test Confusion Matrices

Regard the confusion matrix from the training data below. Ideally, we would like to see a diagonal matrix, indicating that all the predicted targets matched the actual targets. However, that is hardly realistic in the real world, and even the best models get 1 or 2 misclassifications. 

Despite that, we do see the majority of predictions to be on target. Looking at target 4 (row 5), we see that 2 were classified as 0, 5 as 2 and as 3, 1,394 correctly as 4, 20 as 5, 2 as 6, and so on. It appears as the model best predicted target 1, as there were only 8 misclassifications for a true positive rate of 99.51% (1636/(3+1636+3+2)).

Training Confusion Matrix

Next we move to the test set targets and predictions. Again, target 1 has the highest sensitivity in predicting true target 1's at 97.7% (673/(6+673+10)). We will visualize the sensitivities using ROC curves in the post.

Test Confusion Matrix

Now that we have seen how the neural network model predicted the image targets, how well did they perform? To measure the errors and the measure of model fit we turn to our plots, beginning with iterative error.

 Iterative Error
For our first visualization, we can plot the sum of squared errors for each iteration of the model for both the training and test sets. RSNNS has a function called plotIterativeError() which will allow us to see the progression of the neural network training.

Plotting Iterative Error 

As we look at the iterative error plot below, note how SSE declines drastically through the first 20 iterations and then slowly plateaus. This is true for both the training and test values, while the test values (red) do not decrease as much as the fitted training values (black).

 Regression Error
Next, we evaluate the regression error for a particular target, say column 2, which for the numeric target 1 with the plotRegressionError() function. Recall that the numeral targets proceed from 0 to 9.

Observe the targets are categorical, taking values either 0 or 1,while the fitted values from the mlp() model range from 0 to 1. The red linear fit is close to the optimal y=x fit, indicating an overall good fit. Most of the fitted values lie close to 0 when predicting the target value 0, and close to 1 when the target value is 1. Hence the close approximation of  the linear fit to the optimal fit. However, note the residuals on the fitted values, as some vary to 1 when the target is 0 and vice versa. Therefore, the model is not perfect, and we should expect some fitted values to be misclassifications- as seen in the confusion matrices.

 Receiver Operating Characteristic (ROC)
Now we turn to assessment of a binary classifier, the receiver operating characteristic (ROC) curve. From the basic 2 by 2 contingency table, we can classify the observed and predicted values for the targets. Thus we can plot the false positive rate (FPR) with the recall, or sensitivity (true positive rate- TPR). 

Remember that the FPR is the proportion of positive predictions which are actually negative (or 1-specificity), and the TPR is the proportion of positive prediction which are actually positive. With plotROC() we can plot the classification results of the training and test data for target column 3, for the numeral 2.

Plotting ROC Curves for Training and Test Sets

Points above the line of no discrimination (y=x) in a ROC curve are considered better than random classification results. A perfect classification would result in a point (0 , 1), where the false positive rate is 0 and the sensitivity is 1 (no misclassification). 

So when we look at the ROC curve for the training data, we see that the model did pretty well in classifying the target column 3, the image of 2's. The top-left corner approaches a sensitivity of 1, while the false positive rate is close to 0. The majority of 2's were classified correctly, with a few 2's being misclassified as other numbers.

For the test data, we see a slight difference in the ROC curve. There was a small difference in the model classifying 2's correctly, as the test data sensitivity does not approach the high levels as the training sensitivity until it reaches a higher false positive rate. That is to be expected, as the model was fitted to the training data, and not all possible variations were accounted.

Remember that we, established that target column 2, or 1's have the highest sensitivity. We can plot the ROC curve for the test set for the 1's to compare it to the ROC curve of test 2's.

The ROC curve for 1's does reflect our calculations from the test set confusion matrix. The sensitivity is much higher, as more true positive 1's were classified than the 2's. As you can see, the ROC curve for 1's achieve a higher sensitivity for similar values of low false positives, and reaches closer to the top left 'ideal' corner of the plot.

And here is the end of another lengthy post. We covered predicting MNIST handwritten digits using a neural network via the RSNNS package in R. Then we evaluated the model with confusion matrices, an iterative error plot, a regression error plot, and ROC plots.

There is much more analysis we can accomplish with neural networks with different data sets, so stay tuned for more posts!


Thanks for reading,

Wayne
@beyondvalence
LinkedIn



Extra Aside:
Do not be confused by a confusion matrix.

R: Neural Network Modeling Part 1

Hello Readers,


Today we will model data with neural networks in R. We will explore the package neuralnet, and a familiar dataset, iris. This post will cover neural networks in R, while future posts will cover the computational model behind the neurons and modeling other data sets with neural networks. Predicting handwritten digits (MNIST) with multi-layer perceptrons is covered in this post.

The Trained Neural Network Nodes and Weights

So far in this blog we have covered various types of regression (ordinary, robust, partial least squares, logistic) and classification (k-means, hierarchical, random forest) analysis. We turn to neural networks for a new paradigm inspired by imitating biological neurons and their networks. The neurons are simplified as nodes to an input layer, a hidden layer(s), and output nodes.

Let us start R and begin modeling iris data using a neural network.

Organizing the Input Data

First, we require the nnet and neuralnet packages to be loaded in R. Next, we print the first six rows of iris, to familiarize ourselves with the structure. Iris is composed of 5 columns with the first 4 being independent variables and the last being our target variable- the species.

Libraries and Iris

After determining the species variable as the one we want to predict, we can go ahead and create our data subset. Additionally, we notice that there are 3 species grouped together in 50 rows each. Therefore, to create our targets, or class indicators, we can using the repeat function, rep(), three times to generate indicators for setosa, versicolor, and virginica species.

Subset and Target Indicators

Naturally, we will split the data into a training portion and a testing portion to evaluate how well the neural net model fits training data and predicts new data. Below, we generate 3 sets of 25 sample indexes from the 3 species groups of 50 rows- essentially half the data with stratified sampling. Afterwards, we column bind the target indicators with the training indexes to the iris data set we created, again only selecting by training indexes. A sample of 10 random rows are printed below, and note how the species indicator includes a 1 denoting the species type:

Iris Training Data

Training the Neural Network

Now that we have the targets and inputs in our training data we can run the neural network. Just to make sure, verify the column names in the training data for accurate model specification, modifying them as appropriate. 

Using the neuralnet() function, we can specify the model starting with the target indicators: setosa+veriscolor+virginica~. Those three outputs are separated by a hidden layer with 2 nodes (hidden=2), which are fed data from the input nodes: sepal.l+sepal.w+petal.l+petal.w. The threshold is set by default at 0.01, so when the derivative of the sum of squares error-like term with respect to the weights drops below 0.01, the process stops (so weights are optimal).

Neuralnet Training

Plotting the Neural Network

Now that we have run the neural network, what does it look like? We can plot the nodes and weights for a specific covariate like so: 

Visualizing the Neural Network

Hopefully I am not the only one who thinks the plot is visually appealing. Towards the bottom of the plot, an Error of 0.0544 is displayed along with the number of steps, 12122. This Error number is similar to the sum of squares.

Iris Neural Network Nodes

By default, the gwplot() plots the first covariate response with the first output, or target indicator. So below, we see species setosa with sepal length weights. The target indicator and covariate can be changed from default.

Validation with Test Data

How did the neural network model the iris training data? We can create a validation table with the target species and the predicted species, and see how they compare. The compute() function allows us to obtain the outputs for a particular data set. To see how well the model fit the training data, use compute() with the iris.nn data with training indexes. The list component $net.result from the compute object gives us the desired output from the overall neural network.

A Good Fit

Observe in the table above that all 75 cases were predicted successfully in the model. While it may seem like a good result, over-fitting can encumber predictions with unknown data, since the model was trained on the training data. No hurrahs yet. Let us take a look at the other half of the iris data we separated earlier into the test set.

Test Results

Simply take the inverse (-sample.i) of the sample indexes to obtain the mirrored test data set. And look, we did not achieve a perfect fit! Two in group 2 (versicolor) were predicted to belong in group 3 (virginica), and vice versa. Oh no, what happened? Well, the covariates in the training set cannot account for all known and unknown variations in the test covariates. There is likely something the neural network has not seen in the test set, so that it would mislabel the output species. 

This highlights a particular problem with neural networks. Even though the network model can fit the training data superbly well, when encountering unknown data, the weights on the nodes and bias nodes are geared towards modeling the known training data, and will not reflect any patterns in the unknown data. This can be countered by using very large data sets to train the neural network, and by adjusting the threshold so that the model will not over-fit the training data.

And as a final comment, I calculated the root mean square error (RMSE) for the predicted test results and the observed results. The RMSE from this neural network for the test data is approximately 0.23.

RMSE of Test Data

The results are not too bad, considering we only trained it with 75 cases. In the future I will post another neural network, revisiting the MNIST handwritten digits data, which we model earlier with Random Forests.

Stay tuned for more R posts!


Thanks for reading,

Wayne
@beyondvalence

For further reading:

Neuralnet